keropqa.blogg.se - Half adder truth table and circut

#Half adder truth table and circut full

There are many applications of Half Adder and Full Adder. In n bit parallel adder, output carry terminal of one IC would be connected with input carry terminal of next IC.Application of half adder and full adder circuit For n bit parallel adder required number of such ICs are connected together.Ĥ bit parallel adder IC is 4008.

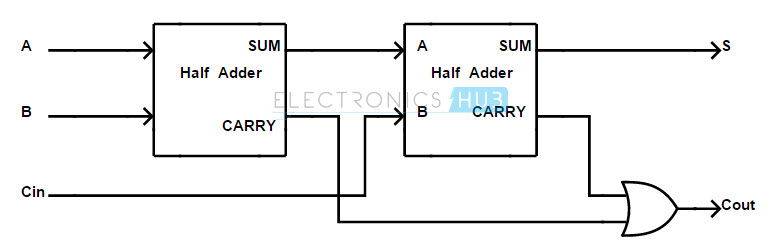
Therefore, final result of the addition would be There are 1 bit, 2 bits and 4 bits parallel adders ICs commercially available in market. The inter connection of 4 full adder in 4bit parallel adder is shown below, Let us examine the justification of the above circuit by taking an example of addition of two 4 bit binary numbers. For adding two 4 bit binary numbers we have to connect 4 full adders to make 4 bit parallel adder. This parallel combination of full adders which performs addition of specific bits binary numbers is called binary parallel adder. This can be done only by connecting as many full adders as the number of bits of the binary numbers whose addition is to be performed. But a single full adder cannot add more than one bits binary number instantly. Hence, from K-maps, Binary Parallel AdderA full binary adder performs addition of any single bit of one binary number, same significant or same position bit of another binary numbers and carry comes from result of addition of previous right side bits of both binary numbers. Hence truth table for all combinations of A, B and C is as follows, From the above table, we can draw K-map for sum (s) and final carry (C out). The carry after addition of same significant bit of augend and addend can represent by C. Any bit of augend can either be 1 or 0 and we can represent with variable A, similarly any bit of addend we represent with variable B. This will continue up to most significant bit of augend and addend.įull AdderFull adder is a conditional circuit which performs full binary addition that means it adds two bits and a carry and outputs a sum bit and a carry bit. Here also we will write sum at final result and add the carry to the next higher significant bits of augend and addend.

After this addition, that is next higher than list significant bit of bits of both binary augend and addend and it is previous carry we get another two bits result.

The LSB of the result is sum and to be put at the list significant position of the final result of the sum, and HSB of the two bits results will be carry and to be added with next higher significant bit of two 4bits augend and addend are 0 and 1 and the carry of previous result i.e.

The LSB of 10 is 0 and higher significant bit (HSB) is 1.

We have to add first list significant bit (LSB) of both 4bits binary number first and this will result a two bits binary number.

The process of binary addition is like follows, Full AdditionBefore knowing about full adder, let us know what is full addition? For that let us consider the example There, are two four bits binary numbers 11 which we have to add. For above K-maps we get, Hence, the logical design of Half Adder would be Although from truth table it is clearly seen that carry (C) column signifies AND operation and sum (S) column signifies XOR operation between input variables but till we went through K-map as it is general practice to do so for more complex binary logic operations. Truth Table for Half Adder K-map for Half AdderNow from this truth table we can draw K-map for carries and sums separately. In first three binary additions, there is no carry hence the carry in these cases are considered as 0. the augend and addend bits, two outputs variables carry and sum bits. Design of Half AdderFor designing a half adder logic circuit, we first have to draw the truth table for two input variables i.e.

The logical circuit performs this one bit binary addition is called half adder. The higher significant bit (HSB) or Left side bit is called carry and the list significant bit (LSB) or right side bit of the result is called sum bit. In one bit binary addition, if augend and addend are 1, the sum will have two digits. Hence, there must be four possible combinations of binary addition of two binary bits In the above list, first three binary operations result in one bit but fourth one result in two bits.